«Fate una creazione matematica! È semplice, è una qualsiasi cosa! Allora ecco: a partire da cifre, da numeri, da punti o da lettere (cioè segni), componete una cosa qualsiasi. Questa qualsiasi cosa tutti sono capaci di farla»
(Le Bohec, 1985).
Queste parole racchiudono la consegna con cui il maestro Paul Le Bohec invitava i suoi alunni/e a produrre un “testo” di matematica completamento libero. Quel «qualsiasi cosa» è interessante perché è naturalmente collegato con la matematica dal bambino stesso e rende così visibile un pensiero spesso già fortemente matematizzato. La creazione diventa un pretesto per lavorare insieme in classe su concetti nuovi, spesso anche “più alti” di quelli normalmente presenti nel curricolo scolastico. Cambia totalmente la prospettiva in cui ci si muove: non è più l’insegnante che delinea a priori un percorso ma si innesca un processo di «devoluzione» attraverso il quale ogni bambino/a fin dall’inizio si sente responsabile del proprio apprendimento. L’insegnante deve essere preparato per saper raccogliere quello spunto e farlo diventare un progetto di ricerca per tutta la classe. Per un adulto può essere spiazzante una consegna così libera ma i bambini e le bambine, soprattutto coloro che sperimentano a scuola un clima non giudicante, accolgono in modo spontaneo un’occasione per sperimentare, formalizzare, rappresentare, comporre e mostrare i concetti appresi o quelli che vorrebbero imparare. Nel 2020 è stato costituito un gruppo di ricerca Nazionale del Movimento di Cooperazione Educativa che ha preso le mosse dai testi di Paul Le Bohec e dal metodo naturale di matematica. Da allora numerose insegnanti hanno provato a lavorare e documentare le loro pratiche e la progettazione delle loro classi si è quindi completamente rispecchiata nei lavori dei bambini, nelle loro intuizioni e nelle rielaborazioni collettive[1].
In questo articolo si darà spazio agli esempi che rappresentano il modo più diretto di comunicare un’esperienza fondata sulla capacità degli insegnanti di documentare e condividere per dire qualcosa di nuovo: le esperienze qui riportate partono tutte dalla creazione di un bambino/a o di un gruppo di bambini/e. Quella creazione diventa l’incipit di un percorso collettivo dove vengono affrontati e appresi nuovi concetti e dove necessariamente si esplorano alcuni degli obiettivi delle Indicazioni nazionali, costruendo un curricolo che è completamente calibrato su ciò che nasce all’interno del gruppo classe.
Al centro del metodo naturale si pone un processo che Freinet chiama tâtonnement del bambino, che è il modo attraverso il quale i bambini e le bambine costruiscono nuove conoscenze, utilizzando ciò che sanno per interpretare, capire ciò che ancora non sanno. È la modalità che permette a bambini/e, anche i più piccoli della Scuola dell’Infanzia, di fare ricerca matematica libera: i bambini e le bambine hanno delle idee e sanno pensare, in modo autonomo, agganciando ogni nuova conoscenza alle precedenti, sanno creare le connessioni giuste per giungere ad un risultato perché la “domanda di partenza” del lavoro di ricerca può nascere soltanto in un contesto basato sull’ascolto e sullo scambio continuo da bambino a bambino e da insegnante a bambino.
In questo articolo ci concentriamo su esperienze fatte alla Scuola Primaria, ma le creazioni matematiche sono molto feconde fin dalla Scuola dell’Infanzia, come si può leggere sul sito del Movimento di Cooperazione Educativa.
Da una creazione ai fondamenti della moltiplicazione
Figura 1. La creazione di M.
Questo percorso si sviluppa in una prima [2] partendo dalla creazione di M. La discussione in classe si apre con la domanda: «Cosa c’è di matematico in questa creazione?»
E.: i pesci! Perché si possono contare. […]
PR.: le cose che ci sono attorno ai pesci.
Ins.: e perché queste cose sono qualcosa di matematico?
G.: i tappi, questi qui, perché si possono contare.
M.: perché sono tre. […]
PI.: si possono contare anche i lati di questo (il rettangolo al centro in alto). […]
R.: i bordi.
A.: puoi contare anche così: 1, 2, 3, 4, 5... (fa scorrere il dito su un lato del rettangolo). Sono tutti i lati.
Ins.: conti un lato dicendo 1, 2, 3, 4, 5… riusciamo a dire cosa stiamo contando? […]
E.: si può contare a pollice, così.
Ins.: forse questo intendeva A., allora non stiamo contando quanti sono i lati. Cosa stiamo contando?
PI: contiamo quanto è lungo… che si fa la lunghezza dei lati.
Da questa discussione emergono due piste di lavoro, la prima sul conteggio di grandezze discrete (i pesci, i tappi…), la seconda il “conteggio” di grandezze continue (lunghezze) che porterebbe verso la misura. Si decide di percorrere la prima pista.
Inizialmente si propongono attività legate al conteggio e alle segnature come nella scuola dell’infanzia, necessarie per non perdere il conto, ma anche proposte più articolate come quella suggerita dalla storia La donnina che contava gli starnuti di Rodari[3] o la seguente, I tesori della classe. Ogni bambino sceglie i suoi “tesori” cercando oggetti nella classe: si tratta di bottoni, feltrini, lego e domino, ma non devono essere più di cinque per tipo; poi, si chiede ai bambini di disporli sul banco in modo che sia facile fare una lista. I bambini allineano gli oggetti e a mano a mano segnano, in genere con crocette o pallini, quanti ce ne sono di ogni tipo. Fare delle liste richiede di passare in rassegna gli elementi uno per uno, capacità alla base del contare. In un momento successivo, data una lista, a ogni bambino si chiede di recuperare il giusto numero di tesori e riordinarli in modo che contarli sia facile e veloce. Con questa e altre attività i bambini capiscono molto presto che contare ad uno ad uno gli oggetti di una collezione richiede molto più tempo che non contare per 2, per 5, per 10. Costruiscono così spontaneamente le prime sequenze “moltiplicative” senza avere ancora piena coscienza del loro significato matematico.
Le attività sul “contare per…” avvicinano i bambini anche a ordini di grandezza maggiori di quelli che riescono normalmente a contare e, soprattutto, imparano presto a contare per gruppi: si fanno i gruppi di tre e si conta quanti gruppi da tre ci sono oppure si spostano gli oggetti a gruppi di due, tre… e si dice: 2, 4, 6… 3, 6, 9. Si costruiscono così delle lunghe strisce verticali con le sequenze numeriche utilizzate, anticipando le tabelline, anche se il significato di moltiplicazione, soprattutto nel suo aspetto relazionale, è ancora da costruire. La conoscenza delle sequenze sarà poi recuperata in un contesto diverso.[4]
Indagine sulla retta numerica
Questo percorso inizia in una classe seconda con le creazioni e viene ripreso nelle classi successive[5] a partire dalla creazione di A. L’insegnante apre la discussione:
Figura 2. La creazione di A
L’insegnante apre la discussione:
Ins. «Che cosa vedete di matematico in questa creazione?»
S. «Secondo me di matematico ci sono i numeri decimali».
G. «Ha usato la tabellina del 2».
N. «Per me ha fatto la tabellina del 2 con i numeri decimali».
A. «Ho deciso di fare la tabellina del 2 per farci stare più numeri cioè per 2».
M. «Dopo lo 0,8 c’è 1,0 poteva scrivere anche solo 1».
N. «Lo zero non vale niente, quindi se lo togliesse non ci sarebbe differenza… se lo togliesse a 0,2 farebbe la differenza… perché 0,2 fa parte dei decimali e se togli lo zero davanti diventano unità… la virgola fa la differenza».
M. «Ma se A. voleva mettere più numeri non poteva fare 0,5… 1… 1,5… 2… 2,5… 3?»
L’ostacolo da superare è il conflitto tra numeri interi e numeri decimali: la retta deve essere decontestualizzata in quanto può rappresentare litri o cioccolata o pizze, in ogni caso grandezze continue. Occorre riprendere l’idea di retta numerica cercando di integrare frazioni e numeri decimali, uscire dai mis-concetti presenti nei bambini, ad esempio “trattare” i numeri decimali come fossero interi, scoprire i centesimi.
L’insegnante propone quindi una creazione a tema a partire dalla creazione di A.: «create due rette numeriche con strisce di carta di lunghezze diverse in cui collocare il numero 3,25. Usate i materiali e gli strumenti che vi sembrano più adatti. Spiegate per scritto come avete fatto a costruirla e perché avete collocato quel numero in quella posizione».
Figura 3. Il prodotto del gruppo 2A
«Per fare la retta ci vuole un’unità di misura». Misurano il filo di lana, 125 cm decidono una distanza di 25 cm tra ogni unità.
Figura 4. Il prodotto del gruppo 2B
Gruppo 2B: «Abbiamo fatto tacche da 0,0 a 4,0. Abbiamo seguito la linea dei numeri decimali sul nostro righello, ogni tacca corrisponde ad un cm. Poi abbiamo messo il 3,25 tra 3,2 e 3,3 perché il 3,25 è un mezzo di un mezzo... significa che dentro a ½ c’è un altro mezzo.»
I bambini e le bambine esprimono chiaramente l’idea che per fare la retta ci vuole una unità di misura; infatti, nel gruppo 3 misurano la lunghezza della striscia e trovano una misura che sia divisibile.
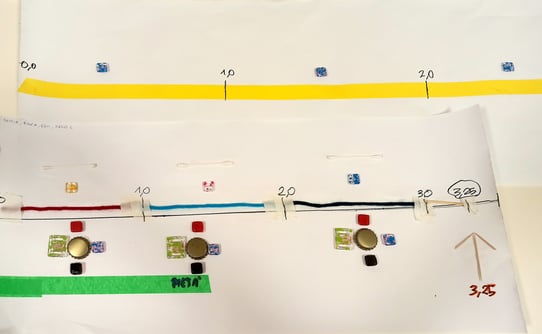
Figura 5. Il prodotto del gruppo 3
Gruppo 3: «Noi abbiamo tirato con il righello una retta. Abbiamo deciso in base alla grandezza del foglio una misura che divisa “per più di 3” stava nel foglio. Abbiamo diviso la distanza tra ogni unità in quattro perché c’è da fare 3,25 e lo 0,25 è ¼ di 1
1:2= 0,50 0,50:2= 0,25 (due importanti pivot cognitivi)
Gli alunni hanno cominciato a rendersi conto della densità della retta numerica, cioè che non esiste un precedente e un successivo perché tra un numero e l’altro ci sono infiniti altri numeri, tema da riprendere in seguito con altre proposte[6] ad esempio riprendere il significato della cifra 5 nella scrittura …,5 che compare collegata con la metà e di associare al linguaggio e al significato la scrittura dei numeri decimali fino ai centesimi (un decimo = 0,1; un centesimo = 0,01).
Il ruolo della corrispondenza scolastica
Una classe seconda[7] di una Scuola Primaria di Milano ha avviato fin dal precedente anno scolastico una corrispondenza con una classe di bambini della stessa età di Mantova. Questa tecnica Freinet crea il terreno ideale per la ricerca e la comunicazione con contesti al di fuori di quello della classe e rappresenta una delle più potenti leve non solo per ricercare in profondità e scrivere in modo sempre più chiaro e completo, ma anche per confrontarsi su una ricerca matematica. La classe di Mantova si accorge del valore del lavoro di ricerca di una loro compagna, H., e decide di comunicare ai corrispondenti l’esito delle sue scoperte cioè che «sommando due numeri pari o dispari si ottiene sempre un numero pari». Per sostenere questa sua intuizione H. riporta molti esempi, classificati in numeri pari e in numeri dispari, e per ogni risultato è indicato se si tratta di un numero pari. Le grandezze dei numeri prese in considerazione sono diverse e questo fa pensare che il funzionamento di operazioni di questo tipo sia sempre uguale e valga per tutti i numeri naturali. Per l’operazione 100+100, H. non scrive il risultato forse perché non è necessario per affermare che sarà sicuramente un numero pari.
Figura 6. La ricerca di H
La ricerca è accompagnata da una lettera collettiva:
«Cari amici di Milano,
[...] questa volta vi scriviamo perché H. ha iniziato una ricerca matematica. Ve la mandiamo perché così anche voi potete fare la ricerca di H... Abbiamo iniziato le ricerche con i depliant[8] ma a volte le idee ci vengono a volte no. Chiediamo anche a voi di dirci qualcosa. [...] »
L’ultima frase esprime il bisogno di una validazione esterna. I bambini di Milano raccolgono la suggestione di H. e dei suoi compagni e, in piccolo gruppo, cercano di capire se le affermazioni della ricerca siano sempre vere. Si riportano alcuni stralci della restituzione dei gruppi alla classe:
A. «Noi abbiamo scritto un numero dispari più lo stesso numero dispari fa un numero pari.»
Ins. «Proviamo a fare degli esempi a partire da quello che ha detto A. per vedere se abbiamo capito quello che ha detto.»
R. «Per esempio 7+7=14»
G. «5+5=10»
Y. «15+15=30»
G. «19+19 = sicuramente è un numero pari!»
A. «Anche un numero dispari più un altro numero dispari diverso fa sempre un numero pari, per esempio 9+11=20»
R. «Due numeri dispari diversi come 9 e 11 danno un numero pari come 20».
A. «Un numero pari più un numero pari uguale o diverso dà sempre un numero pari. 2+2=4, 2+8=10 sono tutti numeri pari».
Dalle interazioni dei bambini emerge l’opportunità di sperimentare la classificazione dei numeri pari e dispari in un contesto di senso, la ricerca di H. viene verificata attraverso numerosi esempi, esempi anche diversi rispetto a quelli riportati nel suo elaborato perché in alcune operazioni gli addendi non sono più uguali, ma si arriva a dire con A. che i numeri dispari che si sommano non necessariamente devono essere uguali tra loro. È molto interessante che un’idea di una bambina di un’altra classe e di un’altra città trovi il contesto per essere approfondita, estesa oppure confutata, così come avviene realmente nelle comunità di ricercatori.
La lettera di risposta ai corrispondenti di Mantova diventa l’occasione per riflettere da un punto di vista metacognitivo su che cosa sia una ricerca matematica:
“Grazie per aver risposto alla lettera, ci è piaciuta tanto la ricerca di H., abbiamo imparato tantissimo anche se abbiamo trovato qualche errorino che H. aveva fatto. […] Secondo noi gli esempi servono per far capire i particolari agli altri, poi una volta che tutti hanno capito, devi spiegare la tecnica in modo che ad altri possano venire in mente altre tecniche”.
Dalle loro parole emerge il valore cruciale dell’esempio per favorire una comprensione profonda della domanda di ricerca e della situazione problematica da risolvere, ma anche la necessità di trovare strategie per “spiegare la tecnica” quindi generalizzare le proprie affermazioni e permettere ad altri di andare avanti.
La ricerca matematica rappresenta allora lo strumento attraverso il quale i bambini possono realmente assumere su di sé il compito della costruzione del sapere a partire dalla proposizione di ciò che sentono il bisogno di indagare e questo genera importanti passaggi nella direzione della generalizzazione dei concetti.
[1] Per approfondire Movimento di Cooperazione Educativa.
[2] Irene Vacca, insegnante di Scuola Primaria.
[3] Cfr. in Merlo (2021) si presenta questa attività che parte da una storia in cui la “donnina” segnava su un taccuino gli starnuti delle persone che incontrava, segni misteriosi che i bambini inventeranno poi per le loro “segnature” in un processo di conta.
[4] Cfr. D. Merlo, A. Cometto, Moltiplicare e dividere, di prossima pubblicazione presso l’editore Carocci.
[5] Antonella Varesi, insegnante di Scuola Primaria.
[6] Cfr. documentazione sul sito del gruppo Creazioni matematiche - Simmetrie numeriche e Creazioni matematiche - Frazioni e decimali sulla retta
[7] Sonia Sorgato, insegnante di Scuola Primaria.
[8] Il depliant, strumento caratteristico della ricerca matematica libera, è un insieme di fogli in formato A4 attaccati tra di loro per non interrompere il flusso della ricerca. La ricerca è poi oggetto di discussione nella classe.
Referenze iconografiche: Chekyravaa/Shutterstock